Creating Cumulative Frequency Distributions

Another important concept related to frequency is cumulative frequency, which keeps a running total of frequencies up to a specific value or class. This provides insight into how data accumulates over a specific range of values, and is fundamental in understanding ideas such as median, quartiles, interquartile ranges, computing area under the uniform, normal, and student T curves. By synthesizing raw data into meaningful patterns, cumulative frequency serves as a stepping stone to deeper statistical concepts, emphasizing the relationship between individual data points and their overall context within a dataset.

Cumulative Frequency

What is Cumulative Frequency?

Cumulative Frequency is the number of data points that are less than or equal to some given number (not necessarily in the data set).

What is a Cumulative Frequency Distribution?

A cumulative frequency distribution is a table that lists either the raw data or classes in the first column and the corresponding cumulative frequencies in the second column.

How do I compute Cumulative Frequency?

Let's turn to our Frequency Distribution about tornado deaths in Tennessee from in How to Create Frequency Distributions:
Frequency distribution table with columns Data and Frequency; Data is Qualitative checkbox selected and column B chosen.
Suppose we are interested in the number of years with 3 or fewer deaths. From the frequency distribution, 32 years had 0 deaths, 10 years had 1 death, 6 years had 2 deaths, and 7 years had 3 deaths. Adding up the number of years gives \[32+10+6+7=55,\] so the cumulative frequency for $3$ is 55. Therefore, 55 years between 1950 and 2023 had 3 or fewer tornado-related deaths in Tennessee.

While it is good to have an idea of how to compute a cumulative frequency, the multiple manual calculations needed for a cumulative frequency distribution increases the likelihood of a calculation error. In our next example, we will see how to use our GeoGebra tool to create a cumulative frequency distribution.

Example

For the data from in How to Create Frequency Distributions, create a cumulative frequency distribution for the raw data.

year, deaths
            2023, 17
            2022, 0
            2021, 4
            2020, 27
            2019, 0
            2018, 1
            2017, 0
            2016, 2
            2015, 2
            2014, 2
            2013, 0
            2012, 3
            2011, 32
            2010, 1
            2009, 2
            2008, 31
            2007, 0
            2006, 34
            2005, 0
            2004, 0
            2003, 12
            2002, 17
            2001, 3
            2000, 1
            1999, 12
            1998, 7
            1997, 1
            1996, 0
            1995, 3
            1994, 5
            1993, 1
            1992, 1
            1991, 5
            1990, 0
            1989, 1
            1988, 6
            1987, 0
            1986, 0
            1985, 0
            1984, 1
            1983, 0
            1982, 0
            1981, 0
            1980, 0
            1979, 2
            1978, 0
            1977, 0
            1976, 0
            1975, 3
            1974, 47
            1973, 1
            1972, 0
            1971, 3
            1970, 3
            1969, 0
            1968, 4
            1967, 2
            1966, 0
            1965, 1
            1964, 0
            1963, 4
            1962, 0
            1961, 0
            1960, 0
            1959, 0
            1958, 0
            1957, 0
            1956, 3
            1955, 0
            1954, 0
            1953, 4
            1952, 75
            1951, 0
            1950, 9

Solution

Load your data into GeoGeobra (see of How to Create Frequency Distributions if you need a refresher).

Frequency distribution table with columns Data and Frequency.

While we can create a relative frequency distribution for the classes, as a first example, it is easier to work with and interpret the rate data. So, we are just going to click on the Cumulative Frequency Checkbox to change the second column from frequencies to cumulative frequencies.

The cumulative frequency distribution for deaths by tornadoes in Tennessee.

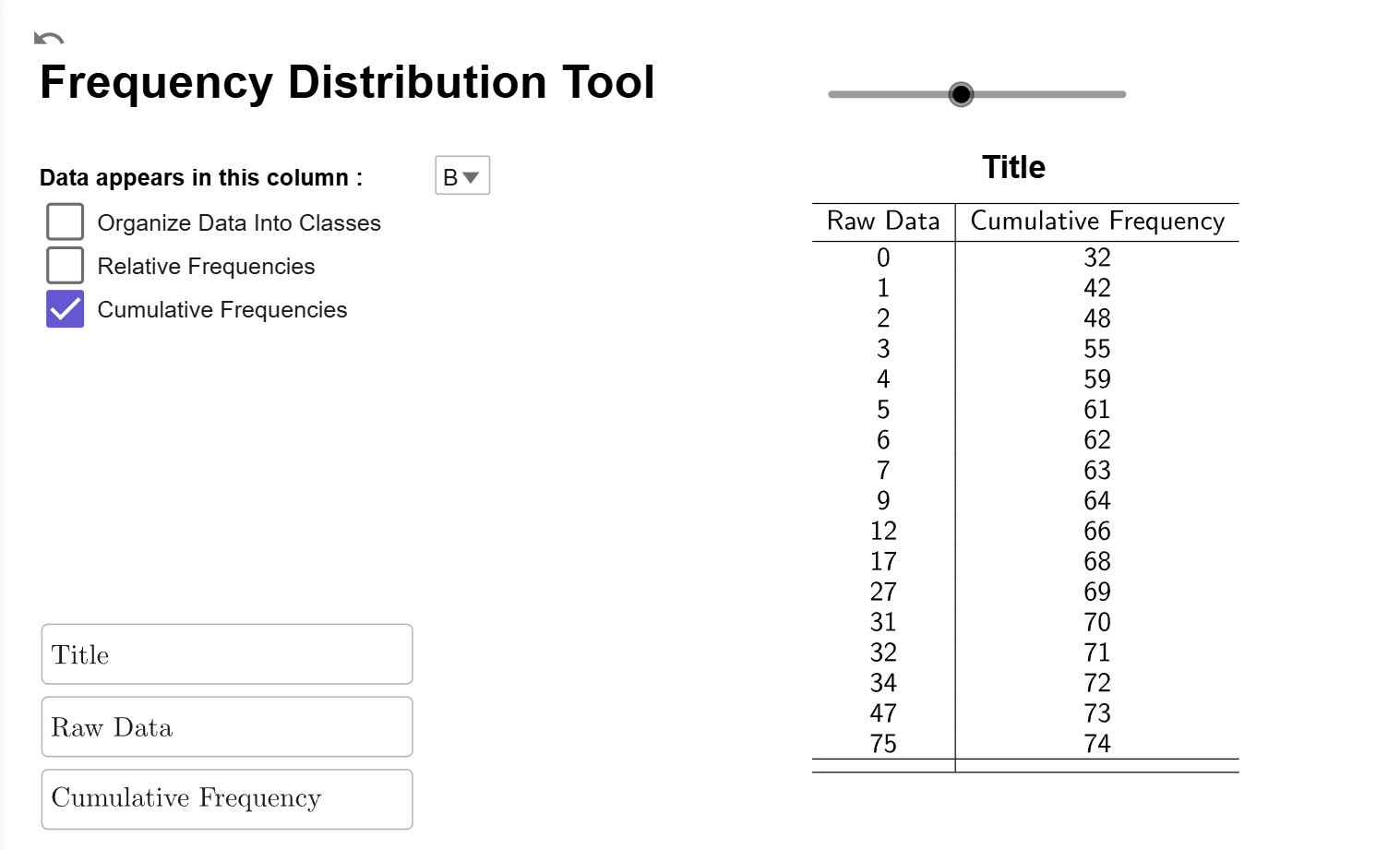
Interpretation

The Raw Data column gives all the unique values of the raw data, listed from smallest to largest. The Cumulative Frequency column tells us the number of years where the death total for the year is less than or equal to the value in the Data column. For example, for $x=17$ deaths, the cumulative frequency of 68 indicates that, between 1950 and 2023, there were 68 years in which the number of deaths caused by tornadoes in Tennessee was 17 or fewer.

$$\tag*{$\blacksquare$}$$

Relative Cumulative Frequency

Relative cumulative frequency, which integrates the concepts of relative frequency and cumulative frequency, offers a powerful tool for understanding data distributions in a statistical context. It represents the percentage of data points at or below a specific value. When we study area under the normal curve later in this course, we will use both cumulative frequencies and relative cumulative frequencies.

What is Relative Cumulative Frequency?

Relative Cumulative Frequency is the percentage of data points that are less than or equal to some given number (not necessarily in the data set). As with relative frequency, we will always express the percentage as a decimal, such as $0.2934$ instead of $29.34$%. Using percentages instead of decimals can cause errors in many of the formulas we will use in this course, as they require values to be expressed as decimals for accurate computation. As a formula, we can express this as \[\text{relative cumulative frequency}=\dfrac{\text{cumulative frequency}}{{n}},\] where $n$ is the number of data points.

What is a Relative Cumulative Frequency Distribution?

A relative cumulative frequency distribution is a table that lists either the raw data or classes in the first column and the corresponding relative cumulative frequencies in the second column.

How do I Compute a Relative Cumulative Frequency?

Let's consider our Cumulative Frequency Distribution from :
The cumulative frequency distribution for deaths by tornadoes in Tennessee.
One useful feature of a cumulative frequency distribution is that the last row provides the total number of data points, which in this case is 74. Now, let’s pick a data point, such as 5. To calculate the relative cumulative frequency, divide its cumulative frequency by the total number of data points: \[\dfrac{{61}}{{74}}\approx 0.8243.\] This means that $82.43\%$ of the years had 5 or fewer deaths. As with relative frequency, we always round to four decimal places.

While it is good to have an idea of how to compute a relative cumulative frequency, the multiple manual calculations needed for a cumulative frequency distribution increases the likelihood of a calculation error. In our next example, we will see how to use our GeoGebra tool to create a cumulative frequency distribution.

Example

For the data from , create a cumulative relative frequency distribution for the raw data.

Solution

For the data from in How to Create Frequency Distributions,

If you are continuing from , the Frequency Distribution Tool should like this:

The cumulative frequency distribution for deaths by tornadoes in Tennessee.

We just need to make sure the Relative Frequencies checkbox is also checked, and it will change the cumulative frequencies column to relative cumulative frequencies. If you have done this correctly, your tool should look like this:

The relative cumulative frequency distribution of the tornado deaths in Tennessee.

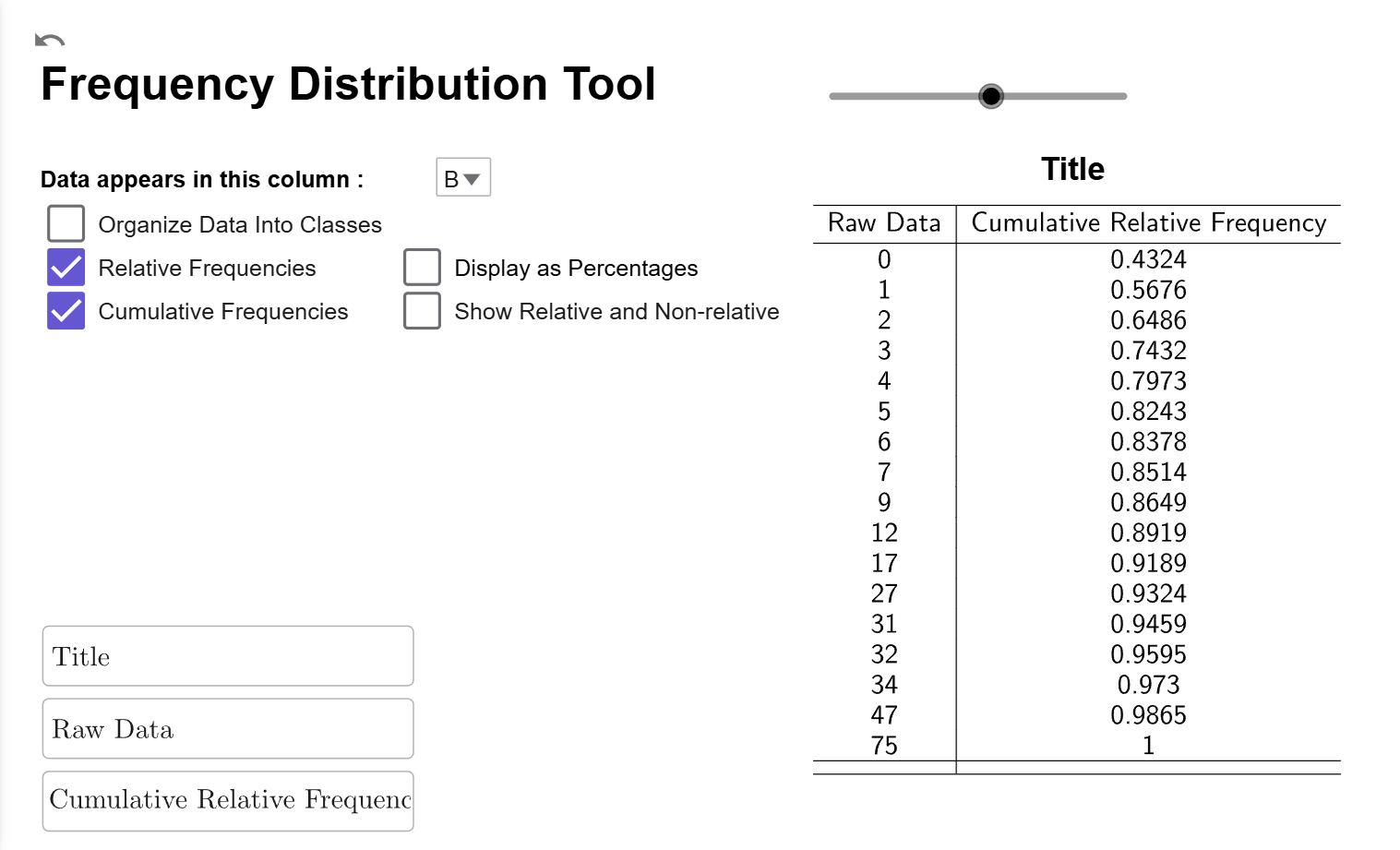
Interpretation

The Raw Data column gives all the unique values of the raw data, listed from smallest to largest. The Relative Cumulative Frequency column tells us the percentage of years where the death total for the year is less than or equal to the value in the Data column. For example, for $x=17$ deaths, the relative cumulative frequency of $0.9189$ indicates that $91.89%$ of the years between 1950 and 2023 had 17 or fewer deaths.

$$\tag*{$\blacksquare$}$$

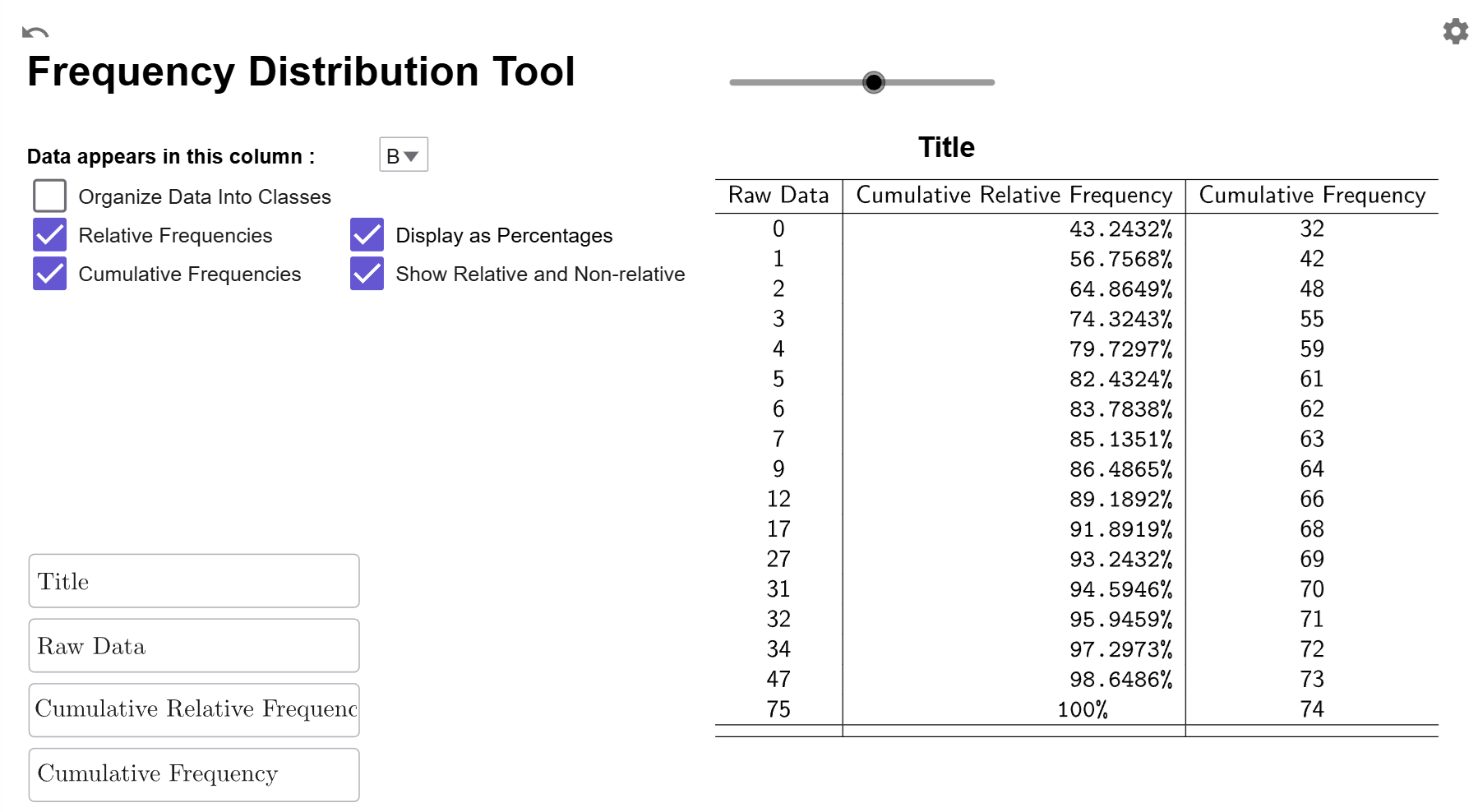
Just like relative frequencies, cumulative relative frequencies can be displayed as percentages or side-by-side with cumulative frequencies.

Relative Frequency Distribution Options

Convert To Percentage

If you click on the Display as Percentages Checkbox, it will convert the relative cumulative frequencies to cumulative percentages.

The relative cumulative frequency distribution with cumulative percentages instead of relative cumulative frequencies.

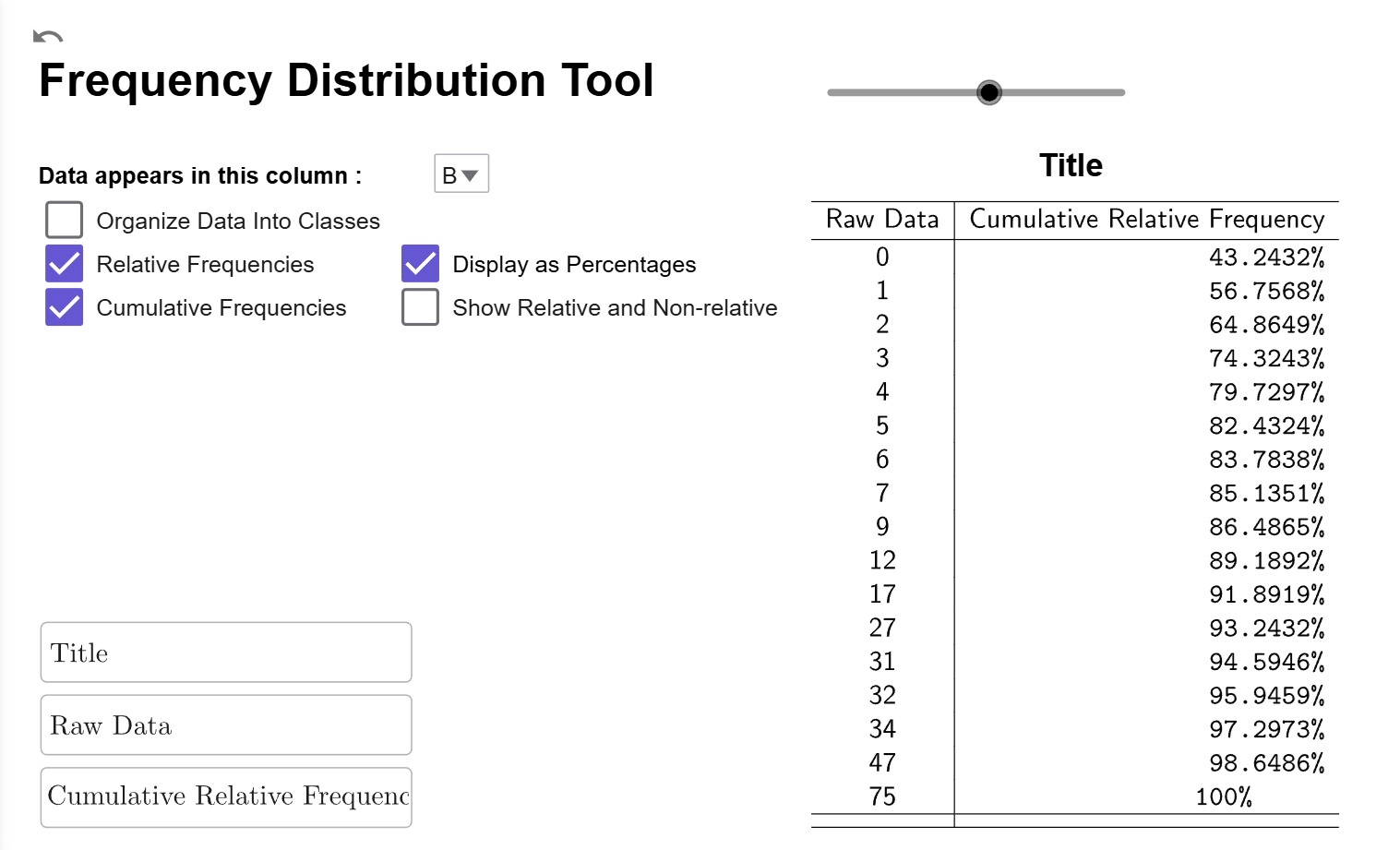
Compare Frequency to Relative Frequency

If you click on the Show Relative and Non-Relative Checkbox, a third column will be added showing the original cumulative frequencies so you can have the cumulative frequency and relative cumulative frequency data side-by-side.

A third column containing the raw cumulative frequencies was added to the cumulative relative frequency distribution.

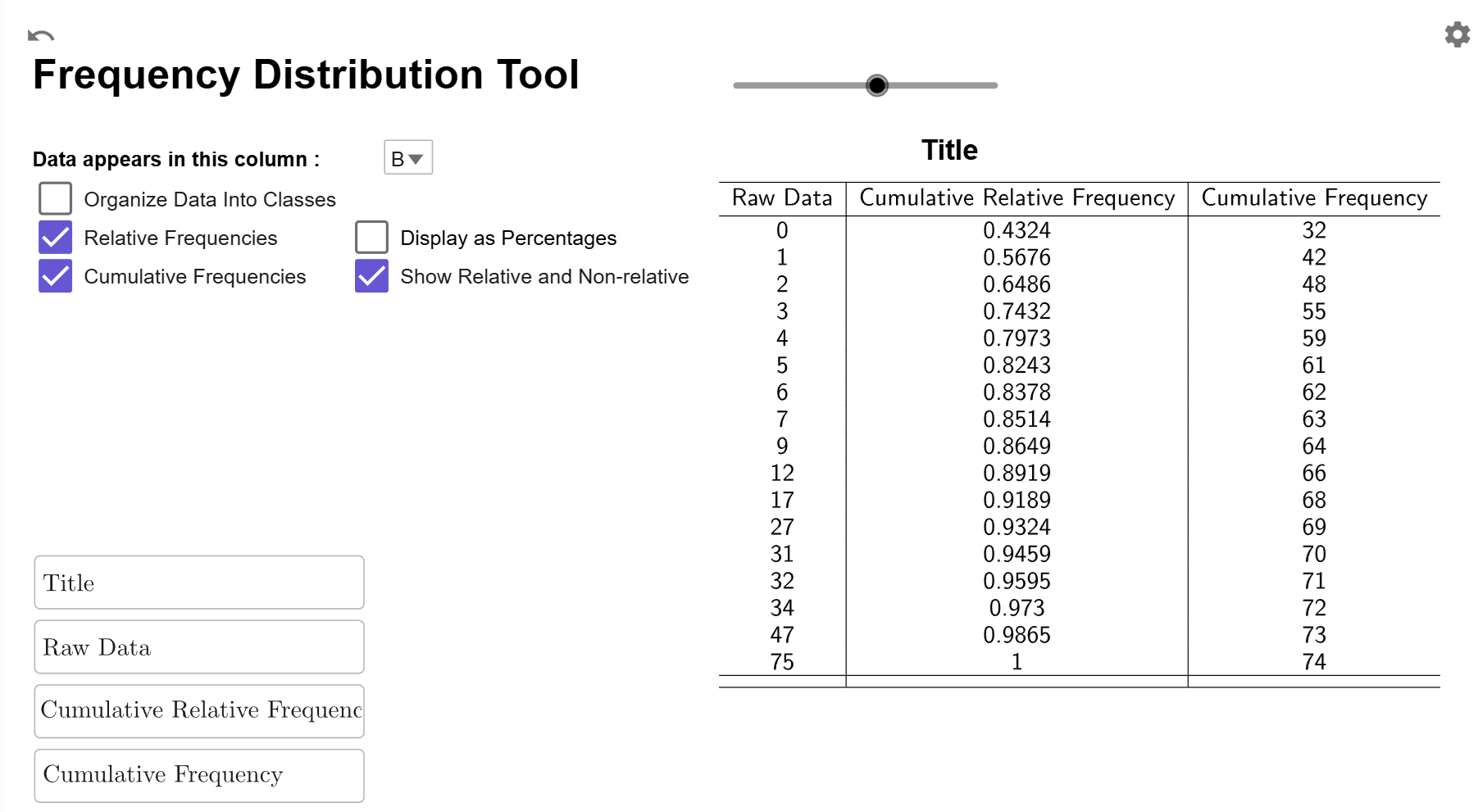
Both Options

You can also select both options at once to compare cumulative percentages to cumulative frequencies.

Both options are checked, allowed comparisons of cumulative percentages and raw cumuluative frequencies.